Michelle Cobeaga
Chemotaxis is defined as the orientation or movement of an organism or cell in relation to chemical agents [1]. For years, scientists have studied this behavior in certain species of bacteria. Through experimentation, they discovered that when motile bacterial cells are placed at one end of a closed capillary tube filled with a medium containing an energy source capable of supporting movement, it is very visible to see that bacteria move preferentially toward higher concentrations of oxygen, minerals, and organic nutrients. This chemotatic behavior produces a sharp and clearly visible gradually migrating band [2]. This paper studies and follows the theory of the traveling bands as proposed by Evelyn Keller and Lee Segel, in which they use partial differential equations to describe the consumption of nutrients and the change in bacterial density due to diffusion and chemotaxis. Collectively, they determine the development and movement of migrating bands. This paper will also analyze and discuss different experiments performed to study chemotatic behavior and their respective results.
The theory in question is the Keller-Segel Theory. Developed by Evelyn Keller and Lee Segel, it presents a phenomenological model for the temporal development of a migrating bacterial band. They model the chemotaxis from a one-dimensional biased random walk, the nutrients being the force which prompts bacterial motion. This motion can be broken down into two alternating states: a straight run of an average duration, followed by an uncoordinated tumble which randomizes the direction of the next run[3,4]. When analyzing this motion and in setting up the partial differential equations describing the nutrient and bacterial concentrations, several things need to be taken into account that are directly associated with the motion: the chemotatic response of the bacteria, the non-chemotactic or diffusive motion of the bacteria, and the bacterial consumption of the nutrients. Diffusion, in this case, is the process in which bacteria moves from a region where their concentration is high to a region where their concentration is low.
The concentration ![]() of the nutrients is modeled by Keller
and Segel's equation
of the nutrients is modeled by Keller
and Segel's equation
![\begin{displaymath}
\frac{\partial s}{\partial t} = -k(s)b + D\left[
\frac{\partial^2s}
{\partial{x^{2}}} \right]\\
\end{displaymath}](img2.gif) |
(1) |
The concentration of nutrients in a closed region ![]() is
is ![]() . Therefore, the concentration of nutrients is changing
according to
. Therefore, the concentration of nutrients is changing
according to
![]() . In this case,
. In this case,
Keller and Segel's corresponding equation for the concentration
of bacteria is
![\begin{displaymath}
\frac{\partial b}{\partial t} = \frac{\partial }{\partial{x...
...rtial{x}}\left[b\chi(s)\frac{\partial{s}}{\partial{x}}\right]
\end{displaymath}](img18.gif) |
(2) |
| (3) |
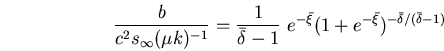 |
(4) |
| (5) |
Much can be learned about the role of chemotaxis on bacterial
motion by comparing experimental results to the the results
produced by the Keller-Segel model. Using their equation for the
speed of migrating bands, Keller and Segel compared speed values
of migrating bands obtained from previous experiments to
calculated values. In once such comparison, a band was observed
to be migrating to higher substrate concentration at 0.9 cm/hr. A
speed of 1.5 cm/hr was obtained using the equation. These results
are reasonably close, with respect to the crude estimates that had
to be made for the values of ![]() ,
,![]() , and
, and ![]() , showing
that the Keller-Segel model provides reliable predictions for band
speed[2].
, showing
that the Keller-Segel model provides reliable predictions for band
speed[2].
Keller and Segel's equation for substrate concentration (3), along
with the measured width of the migrating band, also provided them
with a way to estimate
![]() , the ratio of the
chemotactic strength to motility. Using proper estimates, they
found values of
, the ratio of the
chemotactic strength to motility. Using proper estimates, they
found values of ![]() between 1 and 2. These values give a
numerical measure of the relative strength of chemotaxis. The
values also showed that bands would not appear unless
between 1 and 2. These values give a
numerical measure of the relative strength of chemotaxis. The
values also showed that bands would not appear unless ![]() was
larger than
was
larger than ![]() , because the order of motion produced by
chemotaxis must be large enough to overcome the disordering motion
due to diffusion. Secondly, the values were accurate in that they
also predicted the shape of the bacterial bands. If
, because the order of motion produced by
chemotaxis must be large enough to overcome the disordering motion
due to diffusion. Secondly, the values were accurate in that they
also predicted the shape of the bacterial bands. If
![]() , the front edge of the band was steeper than the lagging edge,
and if
, the front edge of the band was steeper than the lagging edge,
and if ![]() , the lagging edge was steeper. These values
were in agreement with observation[2].
, the lagging edge was steeper. These values
were in agreement with observation[2].
Michael Holz and Sow-Hsin Chen also observed migrating bands of
chemotactic bacteria. In their experiments, they used a photon
correlation spectrometer. This device produced an intensity
auto-correlation function and was used so that the development of
the bacterial density profile could be observed by the scattered
light intensity as the band migrated through a stationary laser
beam. Holz and Chen compared the bacterial density profile
produced by the photon correlation spectrometer with Keller and
Segel's model for travelling bands and made similar comparisons
concerning speed. With proper estimates, their calculated value
for the speed of the migrating band was 0.9 ![]() m/s, and the
observed speed was 0.7
m/s, and the
observed speed was 0.7 ![]() m/s. Their results were relatively
accurate. Similarly, they also calculated
m/s. Their results were relatively
accurate. Similarly, they also calculated ![]() , the
ratio of chemotactic strength to motility. For given values of
, the
ratio of chemotactic strength to motility. For given values of
![]() and of the band width, they obtained a ratio
and of the band width, they obtained a ratio ![]() =
1.72, compared to the expected ratio of 1.33. They also found
that the shape of the band profile was in good agreement with the
shape proposed by the model. For a given ratio of 1.33, the
calculated curves for bacterial density distribution were very
similar to the measured curves predicted by the Keller-Segel
model. It also complied with the prediction that for
=
1.72, compared to the expected ratio of 1.33. They also found
that the shape of the band profile was in good agreement with the
shape proposed by the model. For a given ratio of 1.33, the
calculated curves for bacterial density distribution were very
similar to the measured curves predicted by the Keller-Segel
model. It also complied with the prediction that for
![]() , the back edge was steeper than the front
edge[3]. Altogether, they further showed that the model
represented certain features of the migrating band very
reasonably. However, there were some discrepancies, most likely
due to the assumption of
, the back edge was steeper than the front
edge[3]. Altogether, they further showed that the model
represented certain features of the migrating band very
reasonably. However, there were some discrepancies, most likely
due to the assumption of ![]() = 0 in the Keller-Segel model. The
density profile is either too broad or the speed of migration is
too high when compared to the experiment. It has been found that
when serine was considered as nutrients and
= 0 in the Keller-Segel model. The
density profile is either too broad or the speed of migration is
too high when compared to the experiment. It has been found that
when serine was considered as nutrients and
![]() , the numerical solution was in good
agreement with the Keller-Segel solution. The Keller-Segel model
also predicts a rather uniform thickness of the leading edge for
all values of
, the numerical solution was in good
agreement with the Keller-Segel solution. The Keller-Segel model
also predicts a rather uniform thickness of the leading edge for
all values of ![]() . But the experimental line shape is
fairly symmetric and the leading edge shows variable thickness.
The numerical curves tended to be asymmetric[3].
. But the experimental line shape is
fairly symmetric and the leading edge shows variable thickness.
The numerical curves tended to be asymmetric[3].
Using the photon correlation spectrometer, Holz and Chen also took
into account the presence of tumbling bacteria in formation and movement of migrating bands. They
accomplished this by developing a simple analytical model that
accounts for the contribution of the twiddle motion to the
correlation function. The correlation function was used to analyze
microscopic motility characteristics of the bacteria in the band.
The result was the intermediate scattering function, which
describes the temporal decay of the auto-correlation function and
takes into account both the twiddling and running states of the
bacteria. It allows for the average fraction of bacteria that are
twiddling at a given time to be extracted from the correlation
function:
| (6) |
Holz and Chen furthered the study of migrating chemotactic bands
by continuing their testing of the Keller-Segel model and by
providing means of determining values for the motility (![]() ) and
chemotactic (
) and
chemotactic (![]() ) coefficients of migrating bacteria. They
used a rapid-scanning, light-scattering densitometer that produced
extensive measurements of band migration speeds and band profiles.
To do this, they extended their analysis of the Keller-Segel model
by taking into account
) coefficients of migrating bacteria. They
used a rapid-scanning, light-scattering densitometer that produced
extensive measurements of band migration speeds and band profiles.
To do this, they extended their analysis of the Keller-Segel model
by taking into account ![]() , the substrate diffusion, which was
previously assumed to be zero. They solved the following equation
for the concentration of nutrients, taking into account the
non-zero diffusion coefficient:
, the substrate diffusion, which was
previously assumed to be zero. They solved the following equation
for the concentration of nutrients, taking into account the
non-zero diffusion coefficient:
| (7) |
In conclusion, the movement of travelling bands of chemotactic
bacteria has been successfully discussed and analyzed. Movement
of bacteria is influenced by chemotaxis, a process in which
bacteria seek and move toward regions of higher substrate
concentration. This movement produces highly visible bands of
travelling bacteria. Evelyn Keller and Lee Segel wrote a model to
describe this movement by using partial differential equations to
describe the consumption of the substrate and the change in
bacterial density due to random motion and chemotaxis. They
tested their model experimentally, and obtained reasonably
accurate measurements for the speed and shape of the travelling
bands and also for the ratio of chemotactic strength, ![]() , to
motility,
, to
motility, ![]() . Michael Holz and Sow-Hsin Chen tested Keller and
Segel's model and also produced relatively accurate results for
the ratio of chemotactic strength to motility and for band shape.
They also observed the effects of the twiddling of bacteria in
band movement. They correctly predicted that a large number of
the bacteria are twiddling, as compared to running in a straight
path, at any given time. Additionally, Holz and Chen took into
account the diffusion of the substrate in analyzing the
Keller-Segel model. In doing this, they obtained values for
. Michael Holz and Sow-Hsin Chen tested Keller and
Segel's model and also produced relatively accurate results for
the ratio of chemotactic strength to motility and for band shape.
They also observed the effects of the twiddling of bacteria in
band movement. They correctly predicted that a large number of
the bacteria are twiddling, as compared to running in a straight
path, at any given time. Additionally, Holz and Chen took into
account the diffusion of the substrate in analyzing the
Keller-Segel model. In doing this, they obtained values for ![]() ,
the motility coefficient, and for
,
the motility coefficient, and for ![]() , the chemotactic
coefficient. These values were more accurate than those obtained
when neglecting diffusion. Altogether, Keller and Segel
reasonably modeled and described the actions of travelling bands
of chemotactic bacteria.
, the chemotactic
coefficient. These values were more accurate than those obtained
when neglecting diffusion. Altogether, Keller and Segel
reasonably modeled and described the actions of travelling bands
of chemotactic bacteria.