


Next: About this document ...
Up: An Overview of My
Previous: Riemannian Geometry
What's the difference between a plane and a sphere? Well, for
one, a sphere is curved while a plane is flat.
Another example of a flat space is the cylinder, since we can just
unroll it and it becomes a plane. A sphere can't simply be
unrolled, though. It would need to be stretched to flatten it
out. Unrolling can be done without doing any stretching.
Now in Riemannian geometry we have a way of making this general
concept into a mathematical concept. This is called curvature.
We say a sphere is positively curved. In fact, it
has constant curvature which means the curvature at every point is
the same and positive (whatever that means). Similarly a plane is
flat, so the curvature is zero (whatever that means) at every point.
You might ask what negative curvature means. Negative curvature
is exemplified by a saddle shape, which is the shape of a Pringles
potato chip. If the curvature is negative and the same at every
point, we have what is called Hyperbolic space. This was one of
the first examples of what is called "Non-Euclidean geometry,"
sacrilege to classicists!
Curvature, it turns out, is a very complicated concept, especially
in higher dimensions. It is not completely understood. We do
know that curvature determines the metric and places restrictions
on the topology. Thus if we want to understand our manifold, it
is often easiest to try to understand the curvature. Easier said
than done, though, huh?
So let's give a couple of ideas of what curvature means in two
dimensions. If we draw a triangle in the plane, we find that the
sum of the interior angles is 180 degrees (which is, incidentally
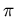 radians and can even be thought of as the definition of
radians and can even be thought of as the definition of
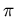 , some number that happens to be approximately
3.141592653589793). No matter which triangle we draw, the sum of
the angles is 180 degrees. But what happens if we draw triangle
on the sphere? Let's say the sphere is really big (like the size
of the Earth) and we draw a little triangle on it, say on the your
driveway. What will the sum of the angles be? They would
essentially be 180 degrees, right? But now let's say we have a
small globe and draw a triangle with a right angle (90 degrees)
at the north pole and whose third side is on the equator. (Recall
that a straight line on the sphere consists of great circles, so
the equator is a straight line and the other two straight lines
are two longitudes meeting at right angles.) Thus we
have a triangle which is essentially one-fourth of the northern
hemisphere or one-eighth of the sphere. What is the sum of the
angles? If you look closely, you see that there are three right
angles! Hence the sum of the angles is
, some number that happens to be approximately
3.141592653589793). No matter which triangle we draw, the sum of
the angles is 180 degrees. But what happens if we draw triangle
on the sphere? Let's say the sphere is really big (like the size
of the Earth) and we draw a little triangle on it, say on the your
driveway. What will the sum of the angles be? They would
essentially be 180 degrees, right? But now let's say we have a
small globe and draw a triangle with a right angle (90 degrees)
at the north pole and whose third side is on the equator. (Recall
that a straight line on the sphere consists of great circles, so
the equator is a straight line and the other two straight lines
are two longitudes meeting at right angles.) Thus we
have a triangle which is essentially one-fourth of the northern
hemisphere or one-eighth of the sphere. What is the sum of the
angles? If you look closely, you see that there are three right
angles! Hence the sum of the angles is
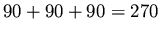 degrees.
It's bigger than 180 degrees! This is what positive curvature
means. If you have a triangle in positive curvature, the sum of
the angles of a triangle is bigger than 180 degrees. Negative
curvature, similarly, means the sum of the angles is less than 180
degrees. You might think about what this means on a Pringles
potato chip! In the standard model of negative curvature, you can
even have triangles which have a sum of angles almost 0!
Another way to think about curvature is in terms of area of disks
with the same perimeter. Let's say we have a circle. What is a
circle? It is the set of points the same distance away from a
single point, say distance 1. (This is rather arbitrary, so we just
choose 1 because it makes the formulas come out better. Hooray!)
This makes sense for any surface with a distance on
it. Now, in flat curvature (the plane), the circle bounds a disk
with area
degrees.
It's bigger than 180 degrees! This is what positive curvature
means. If you have a triangle in positive curvature, the sum of
the angles of a triangle is bigger than 180 degrees. Negative
curvature, similarly, means the sum of the angles is less than 180
degrees. You might think about what this means on a Pringles
potato chip! In the standard model of negative curvature, you can
even have triangles which have a sum of angles almost 0!
Another way to think about curvature is in terms of area of disks
with the same perimeter. Let's say we have a circle. What is a
circle? It is the set of points the same distance away from a
single point, say distance 1. (This is rather arbitrary, so we just
choose 1 because it makes the formulas come out better. Hooray!)
This makes sense for any surface with a distance on
it. Now, in flat curvature (the plane), the circle bounds a disk
with area 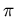 (this is another place where we could have defined
(this is another place where we could have defined
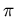 ). Now, suppose the disk was made out of clay and you wanted
to stretch that disk to fit on a
sphere? You'd have to stretch it! Thus the enclosed area is
larger than
). Now, suppose the disk was made out of clay and you wanted
to stretch that disk to fit on a
sphere? You'd have to stretch it! Thus the enclosed area is
larger than 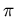 . Now what if you wanted to put it on a Pringles
potato chip? It would be too big and you would have to make the
area smaller. This is another difference between positive and
negative curvature. And the actual curvature relates to how much
you need to stretch or shrink the disk at each point to fit on the
surface.
Now curvature takes place at a point, so we can have positive,
negative, and flat curvature on the same surface. Picture, for
instance, the surface of a doughnut (called a torus). If you
think about it, the outside surface has a positive curvature and
the part inside (the "hole") has negative curvature. In between,
there is some zero (flat) curvature. (Can you guess where? If
it's flat, you should be able to sit a plane on it so that it
touches on a line or anything else with dimension more than just a
point.)
. Now what if you wanted to put it on a Pringles
potato chip? It would be too big and you would have to make the
area smaller. This is another difference between positive and
negative curvature. And the actual curvature relates to how much
you need to stretch or shrink the disk at each point to fit on the
surface.
Now curvature takes place at a point, so we can have positive,
negative, and flat curvature on the same surface. Picture, for
instance, the surface of a doughnut (called a torus). If you
think about it, the outside surface has a positive curvature and
the part inside (the "hole") has negative curvature. In between,
there is some zero (flat) curvature. (Can you guess where? If
it's flat, you should be able to sit a plane on it so that it
touches on a line or anything else with dimension more than just a
point.)



Next: About this document ...
Up: An Overview of My
Previous: Riemannian Geometry
David Glickenstein
2003-12-07