Generalized Crumpling

$\mathcal {S}$ $\subset$ $\mathbb {R}$^m is a domain and the admissible set $\mathcal {A}$ consists of sufficiently regular immersions u : $\mathcal {S}$ $\rightarrow$ $\Omega$ $\subset$ $\mathbb {R}$^d, d $\geq$ m + 1. The energy is given by

$$\mathcal {E} \epsilon \int_{{\mathcal{S}}}^{} \epsilon^{2}_{} \int_{{\mathcal{S}}}^{}$$ (GC)

where P_n is the orthogonal projection onto the normal subspace of immersed manifold u[$\mathcal {S}$].

For $\epsilon$ = 0, we get a nonconvex functional that penalizes deviations from isometry (u is isometric iff Du^{T .} Du = I), and $\mathcal {E}$^$\epsilon$ regularizes this nonconvex energy by penalizing large curvatures. This functional, for general m and d was introduced in [Kra97]. With m = 2, d = 3 it describes many physical systems including thin elastic sheets [WL93,Lob96,BAP97,CM98] and thin-films deposited on substrates [OG94,JK00,BBCDM00,JS01].

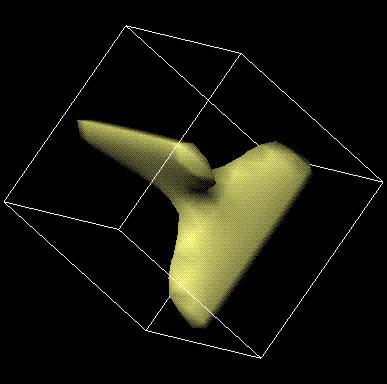
We studied the formation of structures (the analogs of the crumpling ridges) in elastic 3-manifolds when they are crushed in a 4-Space and a 5-Space. The figure above shows the regions of high stretching energy (in material coordinates) in a 3-Cube that is embedded in a 5-Space and has two disclinations at the opposite faces perpendicular to each other.

This work gave insight into the general problems of stress concentration and the formation of nonuniform structures in systems that are forced uniformly. We developed techniques for extracting the dimensions of the singular set on which the energy concentrates from numerical data. In addition, we also obtain geometric conjectures about the ``obstructions'' to the existence of smooth isometric immersions of the unit disk in $\mathbb {R}$^m into a small ball in $\mathbb {R}$^d for d < 2m.

Sound propagation in crumpled sheets

We looked at how sound propagates in crumpled elastic sheets, in particular on the influence of the nonuniform and complex morphology of a crumpled sheet on wave propagation. We derived the effective equation for the propagation of transverse waves in a crumpled sheet. We deduced that the ridges act as barriers to the transport of energy, and waves could thus be ``Trapped'' on the flat facets of crumpled sheets. We tested these effects through direct numerical simulations.