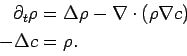Blowup in Parabolic equations and systems

The formation and the dynamics of singularities are important in many contexts ranging from geometry (e.g. the recent work by Perleman on the Geometrization conjecture) to technology (e.g. droplet breakoff in inkjet printers).

In earlier work, we investigated the parabolic-elliptic system of equations

$$\begin{split}\partial_t \rho & = \Delta\rho - \nabla\cdot (\rho \nabla c) \\ - \Delta c & = \rho.\end{split}$$ (KS)

This is a version of the Keller-Segel system that was first introduced to model bacterial chemotaxis. This is a ``generic''' model for a system governing a locally conserved density $\rho$ with the competing effects of dissipation and nonlinear growth. In this sense, it is analogous to other ``generic'' equations - the semilinear heat equation u_t = $\Delta$u + u^p and the Nonlinear Schrödinger Equation - iu_t = $\Delta$u$\pm$| u|²u. Understanding this system will give us insights into the dynamics of more general PDEs which have the same underlying physical mechanisms.

The system (KS) and some variants have been studied by many authors, both in 2D [HV96] and in higher dimensions [BN98,Nag95]. The system exhibits finite time singularities [JL92], and it has self-similar blowup solutions [HMV98] as well as non-self-similar blowup solutions [HV97,HMV97]. For solutions of (KS) on a bounded domain $\Omega$ with no-flux boundary conditions for $\rho$, the quantity $\mathcal {E}$[$\rho$] = $\int_{{\Omega}}^{}$($\rho$log($\rho$) - $\rho$c/2)dx is non-increasing along solutions.

By considering radial solutions on a bounded domain with no-flux boundary conditions, we proved that

Theorem 3   For dimension 2 < d < 10, the system (KS) has the following types of solutions:

1. A family of steady solutions {h_n}_n=0^$\infty$. h_k has k linearly unstable modes.

2. A family of blowup behaviors {H_n}_n=0^$\infty$ for self-similar blow up with parabolic scaling (solutions converging to a profile in the scaled variable $\eta$ = r/$\sqrt{{T-t}}$ where T is the blowup time of the solution). H_k has k + 1 linearly unstable modes in similarity coordinates, $\eta$ and $\tau$ = log(T - t) (not the usual ``fixed'' (r, t) coordinates).

3. Additional blowup behaviors H_* (parabolic scaling), and S (non-self-similar).

Item 2 brings up the following question, whose answer is not known in general:

Problem 5   What is the connection between the linear stability/instability of a solution in similarity variables, and notions of stability in ``fixed'' coordinates?

On the basis of numerical evidence, we offer the following plausible conjecture:

Conjecture 3   The initial data that asymptote to the similarity solution H_n have codimension n. In particular, the solution H₀ is robust, and can be observed for generic initial data.

Numerical simulations show that the solutions H₀, h₀ and S can be observed for generic initial conditions. u₀ and u₁ are initial data leading to distinct generic asymptotic solutions. Considering a one parameter family of initial data interpolating between u₀ and u₁, we can (numerically) determine the basin boundaries for the solutions h₀, H₀ and S using a bisection procedure. We find that initial conditions on the basin boundaries lead to solutions that asymptote to H₁, h₁ or H_*.

h₁, for example, lies on the boundary of the basins of H₀ and h₀. Thus, there exist sequences of initial conditions converging to h₁ that lead to solutions asymptoting to h₀, and likewise for H₀. By analogy with finite dimensional flows, we say that h₁ has connections to h₀ and H₀. Figure 2 summarizes all the connections observed numerically for (KS) [BCK⁺99]. We conjecture that these connections can be understood through a Morse theory of the underlying energy landscape, and that

Conjecture 4   The solutions h_n and H_n of (KS) are codimension n, and they have connections to the (2n) solutions h₀,..., h_n-1 and H₀,..., H_n-1.

Figure 2: Connections

Figure 2 summarizes the connections that we observe numerically (the solid lines) and also some of the connections whose existence we conjecture (the dashed lines).

This is a surprising similarity between the infinite dimensional PDE and Morse theory for finite dimensional dynamical systems. For the PDE, the asymptotic states are described by the various blowup modes, the steady solutions, and their ``unstable manifolds''. This is analogous to the $\omega$-limit sets for finite dimensional gradient flow which consists of equilibrium points and their unstable manifolds. This analogy is not just qualitative, but also gives quantitative predictions, e.g. for the blowup time of a solution.

A similar connection with finite dimensional dynamical systems is also observed in the numerical simulations of Einstein's equations for initial conditions at the threshold of collapse to black-hole formation. This phenomenon gives us an approach to investigate the important cosmic censorship conjecture which postulates that there are no ``naked'' black hole singularities.

In recent work, Merle and Zaag have classified all the connections for the semilinear heat equation, and they use these results to develop a dynamical systems approach to the stability of blowup in the semilinear heat equation. I am working on the analysis of the (KS) system using some of their techniques and hope to develop a similar theory for this equation.