


Next: Riemannian Geometry
Up: An Overview of My
Previous: My view of differential
In this section we are going to describe the general class of
things we want to study. We are going to start with a large class
of things and then add more and more structure to it so that it is
more and more limited. In mathematics we often are interested in
classifying objects up to some form of equivalence. For instance,
we may want to be able to distinguish TYPES of US coins. In other
words, we want to know how many different types of coins there
are, and if we have two, we want to know, for instance, if they are both pennies
or if one is a nickel. A mathematician might call this
classifying up to the type of coin (this is the equivalence). To
contrast, we may want to classify up to type of coin and year it
was minted. In the first case, if we have a 1986 penny and a 1997
penny, they are the same up to equivalence. But in the second
case they would be different up to equivalence. Thus it is
important to know what we consider to be the same and what we
consider to be different. In the first case, our equivalence was
very weak, since we only consider two things different if they
were different types of coins. Thus the only objects we have are pennies, nickels, dimes, quarters,
half dollars, and dollars (6 objects total). In the second case our equivalence
was stronger because we consider two things different if their
years of minting are different. In this case we have a lot of
different objects, including 1999 pennies, 1990 pennies, 1987
dimes, 2000 nickels, 1967 quarters, 1990 dimes, etc.
Now we are going to consider objects the same based on a number of
different equivalences. With manifolds, we are mostly going to be
concerned with two being "topologically" the same and being
"geometrically" the same. These two terms are actually not as
specific as we might hope, but I don't want to get into the
specifics of different kinds of topological equivalence or
geometric equivalence. I will describe the relevant ones.
Now the idea of two things being topologically the same is perhaps
one which you have not encountered before. Two things are
topologically the same if they have the same shape in the sense
that one can be deformed into the other one without "breaking" it.
I'm being a little vague because the actual definition is not
very instructive to the beginner. But you already understand the
basics of this concept. Now consider if you had a perfect circle
that you drew with a compass and a circle that you drew freehand.
Now only one is REALLY a circle, right? The other one isn't a
perfect circle in that there is no one point in the center which
is EXACTLY the same distance from every point on the circle. But,
nonetheless, if you were to show it to someone, they would
recognize it as a circle, even though it's not a circle. This is
in some sense the difference between being topologically the same
and geometrically the same. Geometrically, the second is not a
circle, since there is no center. But topologically they are
equivalent. Topologically both are the same, because we could
change one of the "circles" slightly to make it into the other.
Now when I say change, I am only allowing certain kinds of
changes. For instance, you are not allowed to cut the circle
unless you reattach the two ends to each other. So, for instance,
if your circle were a rubber band you could stretch it but not let
it break. You could even cut it, tie a knot in it, and reattach
the two ends. These would all be topologically equivalent. This
idea that you can stretch things however much you want has caused
topology to be dubbed clay geometry. The typical example given is
that topologically a coffee mug is the same as a doughnut. (Think
about why!) But really we just removed some of our restrictions
on two things being the same.
We are just about ready to learn what a manifold is. We first
need to understand what Euclidean space is. You already know what
Euclidean space is. It's just what you consider to be space. For
instance, the infinite line (number line) is a Euclidean space.
So is the infinite plane. So is the space we live in. So what is
it exactly? Well, the number line is just the set of all real
numbers (so we allow all decimal expansions, even infinite ones
that give irrational numbers like 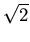 and
and 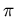 ). This is
one dimensional Euclidean space since there is only one degree of
freedom. You can only go forward or backward if you live on the
line. Now consider the plane. Here we have two degrees of
freedom. We can go forward/backward or left/right. This is two
dimensional Euclidean space. It is important that
forward/backward is not the same direction as left/right, for then
we would have a line, right? Now, if we want to describe a
location on the plane, we can fix a point and then say how far
forward/backward to go and how far left/right to go. Thus there
are two real numbers associated to a position in the plane. This
is what we really mean by two degrees of freedom or two
dimensions. Now in space we have three directions we can go:
forward/backward, left/right, and up/down. Thus we get three
dimensional Euclidean space. You can similarly imagine Euclidean
space of any dimension. All you need is some number of different
degrees of freedom and a location (called a point) is determined
by that many different numbers, which tell you how far you are in
each direction from some fixed point which we will call the origin
(note that the origin is 0 units away from itself in all
directions). Note that topologically the size of the units is
unimportant.
Now a manifold is just something which locally looks like
Euclidean space. Consider, for instance, the surface of the
Earth. For ages it was believed to be a plane. Why? Because
from what we can see it is a plane. (Topologically, hills,
mountains, and valleys don't change this, right?) But we know
that it actually curves back on itself and is topologically a
sphere instead of a plane. So it is a manifold. Locally it looks
like a plane (Euclidean two dimensional space). We would call it
a two dimensional manifold because it is locally like two
dimensional Euclidean space.
Now here is a question: is the universe we live in Euclidean
three space or is it some other three dimensional manifold? As
far as I can tell, this is still unknown. One goal of mathematics,
however, is to see what it could possibly be and then maybe we
could eliminate things on the list with experiments. (This is,
of course, under the assumption that the everywhere in the universe looks
essentially like the way we see it, which seems a reasonable
assumption.)
). This is
one dimensional Euclidean space since there is only one degree of
freedom. You can only go forward or backward if you live on the
line. Now consider the plane. Here we have two degrees of
freedom. We can go forward/backward or left/right. This is two
dimensional Euclidean space. It is important that
forward/backward is not the same direction as left/right, for then
we would have a line, right? Now, if we want to describe a
location on the plane, we can fix a point and then say how far
forward/backward to go and how far left/right to go. Thus there
are two real numbers associated to a position in the plane. This
is what we really mean by two degrees of freedom or two
dimensions. Now in space we have three directions we can go:
forward/backward, left/right, and up/down. Thus we get three
dimensional Euclidean space. You can similarly imagine Euclidean
space of any dimension. All you need is some number of different
degrees of freedom and a location (called a point) is determined
by that many different numbers, which tell you how far you are in
each direction from some fixed point which we will call the origin
(note that the origin is 0 units away from itself in all
directions). Note that topologically the size of the units is
unimportant.
Now a manifold is just something which locally looks like
Euclidean space. Consider, for instance, the surface of the
Earth. For ages it was believed to be a plane. Why? Because
from what we can see it is a plane. (Topologically, hills,
mountains, and valleys don't change this, right?) But we know
that it actually curves back on itself and is topologically a
sphere instead of a plane. So it is a manifold. Locally it looks
like a plane (Euclidean two dimensional space). We would call it
a two dimensional manifold because it is locally like two
dimensional Euclidean space.
Now here is a question: is the universe we live in Euclidean
three space or is it some other three dimensional manifold? As
far as I can tell, this is still unknown. One goal of mathematics,
however, is to see what it could possibly be and then maybe we
could eliminate things on the list with experiments. (This is,
of course, under the assumption that the everywhere in the universe looks
essentially like the way we see it, which seems a reasonable
assumption.)



Next: Riemannian Geometry
Up: An Overview of My
Previous: My view of differential
David Glickenstein
2003-12-07