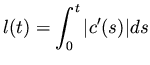Next: Curvature
Up: An Overview of My
Previous: What is a manifold?
We have described what we are looking at topologically, but we
are also interested in geometry. Riemannian geometry is one way
of looking at distances on manifolds. This seems an easy enough
concept when you first think of it, but after further though we
realize it is not so easy. Sure we know how to measure distances
on a plane. The shortest distance between two points is a
straight line, right? So just draw the line and measure the
distance (first we set what unit measure is, for instance 1 meter,
and then compare the distance we want to measure to our set
standard unit distance, say the meter stick). But on a sphere how
do we measure distance? Or on a torus (the surface of a
doughnut)?
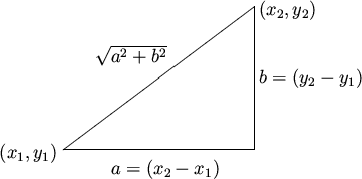
A sphere we can think of as living in Euclidean 3-space and then
just say that the distance between 2 points on the sphere is just
the distance between those points in 3-space, as described by the
Pythagorean theorem, which says that for points  and
and
 the distance between them is
which is the fact that the length of the hypotenuse (longest side)
of a right triangle is equal the square root of the sum of the
squares of the other two sides.
the distance between them is
which is the fact that the length of the hypotenuse (longest side)
of a right triangle is equal the square root of the sum of the
squares of the other two sides.
In addition, we can
change this slightly by deforming the sphere in 3-space so that it
is still topologically a sphere but not geometrically a perfect
sphere.
This is a perfectly legitimate way to define distances.
It has one disadvantage, however. It requires that the sphere be
"embedded" in 3-space. In other words, we can think of the sphere
as living in 3-space, but maybe our geometric sphere cannot live
in 3-space. This concept is a little weird in the case of the
sphere, so let's look at this problem one dimension down.
Consider the circle. Now, we can think of the circle as living in
Euclidean 2-space (the plane). Now I claim that we can find
topological circles that we cannot put in Euclidean 2-space!
These are called knots and they are exactly what you consider to
be knots. Take a circle, then disconnect it, then tie a knot in
it, then reattach the ends. We now still have a topological
circle. If you lived on the circle, your couldn't tell the
difference than if there was no knot tied in it. But we can't
crunch the knot down so it lives in the plane. Thus we need to
have the circle live in 3-space and we are fine.
So we need to first know which sized (dimension) Euclidean space
we live in to use this method. Of course, there is no reason to
believe that any manifold lives in some appropriately sized
Euclidean space, although this fact is true (but hard to show).
We are going to skirt these issues by taking another approach to
distances.
Suppose we could measure the length of curves. Then we could
simply define the distance between two points to be the length of
the shortest path, if one exists. Even if one does not exist, we
could express the distance as the largest lower bound for lengths
of paths between the two points (this is called the infimum).
This isn't too important so let's assume that we can find a
shortest path.
So we could measure distances if we could measure the lengths of
paths. This is where a Riemannian metric comes in. So if you are
driving, how would you measure the distance you traveled? Well,
one way is to look at your speedometer and remember how fast you
are going at every point and then consider how long it took you to
get where you were going. Since speed is just distance per unit
time (like miles per hour) we just multiply the speed times the
time and we get the distance. That's how far we traveled. The
only problem is that our speed changes and our direction changes,
so we actually need to take into account which direction we are
traveling (this means using the velocity vector instead of just
the speed, which is the length of the velocity, ignoring
direction). Also, our formula only works if the velocity does not
change. But our velocity changes. What do we do? We chop our
time intervals up into smaller segments which have constant
velocity. This doesn't quite work because there is no time when
we are going at a constant velocity (most likely), but as we chop
up the time interval more and more, our approximation is more and
more accurate. In the limit, we end up with an integral and can
calculate the actual length by computing that integral (this
involves some basic calculus). For culture, let's look at how we
would write this:
which we read as the length  of the curve (path)
of the curve (path)  is the sum
(the integral sign
is the sum
(the integral sign 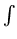 is a German 's' standing for sum) of the
speed of the curve, denoted
is a German 's' standing for sum) of the
speed of the curve, denoted  , multiplied by a really
small length of time, denoted
, multiplied by a really
small length of time, denoted 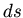 . The the term
. The the term  just means we measure
the path from time 0 to time
just means we measure
the path from time 0 to time 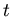 . Anyway, the what we get out of this
discussion is that only need to know the
velocity at every point.
The velocity at every point can be considered as a vector (arrow)
indicating where we are going (direction) and at what speed. It is tangent to
our path because it tells us which direction to move.
And it is only defined at each point. We just need to
be able to measure these velocities and then we can compute
lengths of curves. Thus we need to be able to measure the length
of vectors at every point. This is what a Riemannian metric does.
It provides us with a way of measuring vectors at every point.
Since these are local things and we understand what vectors at
different points in Euclidean space are, we can do the same things
on manifolds, since locally they look like Euclidean space.
So the Riemannian metric is a function defined at every point that
takes two vectors and gives a number. Technically, a Riemannian metric must be a symmetric bilinear form (otherwise it is called
a Finsler metric). This condition isn't too important for
us to understand at this point, but it is easy to state so why
don't we do it anyway. We express the Riemannian metric as
. Anyway, the what we get out of this
discussion is that only need to know the
velocity at every point.
The velocity at every point can be considered as a vector (arrow)
indicating where we are going (direction) and at what speed. It is tangent to
our path because it tells us which direction to move.
And it is only defined at each point. We just need to
be able to measure these velocities and then we can compute
lengths of curves. Thus we need to be able to measure the length
of vectors at every point. This is what a Riemannian metric does.
It provides us with a way of measuring vectors at every point.
Since these are local things and we understand what vectors at
different points in Euclidean space are, we can do the same things
on manifolds, since locally they look like Euclidean space.
So the Riemannian metric is a function defined at every point that
takes two vectors and gives a number. Technically, a Riemannian metric must be a symmetric bilinear form (otherwise it is called
a Finsler metric). This condition isn't too important for
us to understand at this point, but it is easy to state so why
don't we do it anyway. We express the Riemannian metric as 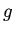 and we
express vectors at a point
and we
express vectors at a point 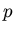 in our manifold as
in our manifold as
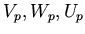 .
then we can measure quantities like
.
then we can measure quantities like
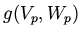 . The fact that is
symmetric means:
and bilinearity (when coupled with symmetry) is
the following condition:
But you probably don't have to understand this too much. I just
get carried away sometimes.
So the important thing is that the Riemannian metric gives us a
way to measure lengths of vectors at each point in the manifold,
and also gives us a way of measuring lengths on the manifold.
. The fact that is
symmetric means:
and bilinearity (when coupled with symmetry) is
the following condition:
But you probably don't have to understand this too much. I just
get carried away sometimes.
So the important thing is that the Riemannian metric gives us a
way to measure lengths of vectors at each point in the manifold,
and also gives us a way of measuring lengths on the manifold.



Next: Curvature
Up: An Overview of My
Previous: What is a manifold?
David Glickenstein
2003-12-07