Nonlinear diffusion equations with discontinuities

We investigated the following non-linear discrete diffusion equation on a lattice

$$\left[\vphantom{ \mathrm{Int}[u_{i-1}(n)] - 2\,\mathrm{Int}[u_{i}(n)] + \mathrm{Int}[u_{i+1}(n)] }\right. \left.\vphantom{ \mathrm{Int}[u_{i-1}(n)] - 2\,\mathrm{Int}[u_{i}(n)] + \mathrm{Int}[u_{i+1}(n)] }\right]$$ (A1)

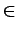
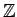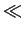where i, n $\in$ $\mathbb {Z}$ and Int[x] denotes the greatest integer that is less than or equal to x. This equation is a reduction of a Frenkel-Kontorova model, and it arises in a physical model for Charge-Density-Wave (CDW) systems. We are particularly interested in the regime where k $\ll$ 1.

Figure 3: Dynamics of the model

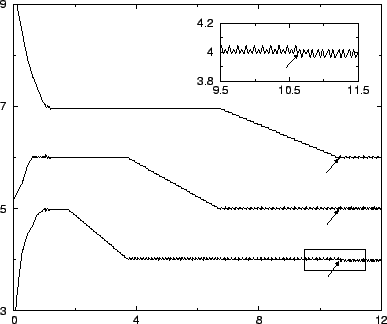Figure 3 shows the evolution of the variables u_i on three consecutive sites in a lattice consisting of 8 sites with k = 3 x 10^-2. The horizontal axis is the scaled time t = kn. The arrows indicate a simultaneous change in the oscillation patterns. The inset is a blowup of the area in the box.

As we show, and illustrate in Fig. 3, the system has an interesting ``stick-slip'' behavior:

1. If u_i(n) is not close to an integer, the site u_i is ``free'', i.e. the dynamics of u_i is very similar to the dynamics in the linear discrete diffusion equation u_i(n + 1) = u_i(n) + k$\left[\vphantom{ u_{i-1}(n) - 2 u_{i}(n) + u_{i+1}(n) }\right.$u_i-1(n) - 2u_i(n) + u_i+1(n)$\left.\vphantom{ u_{i-1}(n) - 2 u_{i}(n) + u_{i+1}(n) }\right]$.
2. If u_i(n) is close to an integer m, then u_i can become ``stuck'' for a time t = O(1) and oscillate while remaining within O(k) of m. Also, consecutive sites can be stuck simultaneously executing coherent periodic motions.
3. For the ``stuck'' sites, the oscillation pattern (the ``microstructure'') can change at transitions which are ``nonlocal'' in that the behavior of a whole string of sites changes simultaneously. Fig. 3 displays one such transition near t = 10.5.

We obtained a continuous time limit of the system in (A1) using the maximum principle for parabolic equations, that is we showed convergence of the sequence of solutions as k $\rightarrow$ 0 and derived the appropriate Homogenized equation.

Specifically, we show that by rescaling the discrete time index to get a continuous time variable t = kn, the solutions u_i(n) converge uniformly as k $\rightarrow$ 0. We also derive the appropriate dynamical equations for the limiting functions.

This motivates the following:

Problem 6   Continuous time limit: Consider the system of difference equations

$$\left[\vphantom{ f_{i-1}(u_{i-1}(n)) - 2 f_{i}(u_{i}(n)) +f_{i+1}(u_{i+1}(n)) }\right. \left.\vphantom{ f_{i-1}(u_{i-1}(n)) - 2 f_{i}(u_{i}(n)) +f_{i+1}(u_{i+1}(n)) }\right]$$ (A2)

where each f_i is a possibly discontinuous, nondecreasing function. Show that, the scaled solutions u_i(Int[t/k]) converge uniformly on compact intervals [0, T]. Also, formulate appropriate dynamical equations for the limit functions.

Another interesting feature of this system is the transitions between different kinds of ``microstructure'' (the oscillation patterns for the stuck states). This naturally suggests the interesting question:

Problem 7   Equations of the form (A2) arise in distributed control systems where the controllers are quantized and necessarily discontinuous.

Another importantr question is to characterize the various oscillation patterns and the transitions that are observed in (A1), or more generally in (A2). This is an example of a dynamical system with an evolving microstructure.